Dancing Links Sudoku

One of the first projects I did when I started learning python was building a solver for sudoku.

Empty board: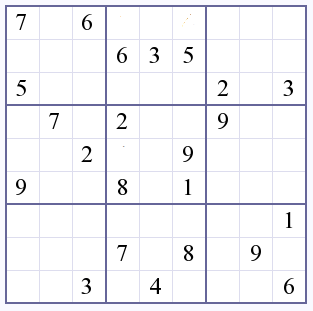
 Completed board: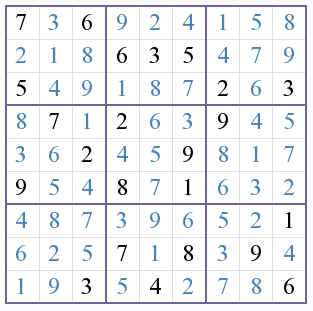

This is a pretty well understood space, which made it a nice learning project. The two styles of computer sudoku solvers are depth-first searches or ones that attempt to solve the puzzle similar to a human. This one is a depth-first search, which means it is pretty much guaranteed to reach an answer eventually.

The ones that atrempt to use different techniques to solve like a human can end up giving a grade of difficulty, based on which techniques are needed to solve it. I stopped this project before figuring out if it could grade a puzzle.

It implements Donald Knuth’s Dancing Links algorithm, which is a pretty readable paper and kind of fun. I also love that Donald Knuth publishes papers as .PS files.

I ended up playing with a lot of python tricks to wring speed out of it, most of which are probably unnecessary. It is also capable of printing out a copy of the board and decision tree, which helps to visualize a bit how it’s doing what it’s doing. (Though the graph isn’t super readable)

Overall this was a fun project and a good learning exercise.

View Full Size

Caption:

  • (Row, Column), (Attempting to place #)
  • P.0,7 = Square in position 0, 7 has no allowable values
  • R.6-5 = Row 6, cannot place 5
  • B.8-5 = Block 8, cannot place 5
  • C.6-5 = Column 6, cannot place 5

To run this code, use sudoku.py -p [puzzle] with the blanks puzzle being separated by “.”, ie:

% python sudoku.py -p 7.6.........635...5.....2.3.7.2..9....2..9...9..8.1...........1...7.8.9...3.4...6
-------------------------
| 7 . 6 | . . 4 | . . . |
| . . . | 6 3 5 | . . . |
| 5 . . | . . 7 | 2 . 3 |
-------------------------
| . 7 . | 2 . . | 9 . . |
| . . 2 | . . 9 | . . . |
| 9 . . | 8 . 1 | . . . |
-------------------------
| . . . | . . . | . . 1 |
| . . . | 7 . 8 | . 9 . |
| . . 3 | . 4 2 | . . 6 |
-------------------------
-------------------------
| 7 3 6 | 9 2 4 | 1 5 8 |
| 2 1 8 | 6 3 5 | 4 7 9 |
| 5 4 9 | 1 8 7 | 2 6 3 |
-------------------------
| 8 7 1 | 2 6 3 | 9 4 5 |
| 3 6 2 | 4 5 9 | 8 1 7 |
| 9 5 4 | 8 7 1 | 6 3 2 |
-------------------------
| 4 8 7 | 3 9 6 | 5 2 1 |
| 6 2 5 | 7 1 8 | 3 9 4 |
| 1 9 3 | 5 4 2 | 7 8 6 |
-------------------------
Found 1 solution(s) in 0.007 seconds.

social